A derivative is a gist of calculus and its working is to check the sensitivity to a difference in the result with respect to a change in its given value. For example, the derivative of the position of the object which is in motion with respect to time is the velocity of the object it tells when time increases the position of the object changes rapidly.
The two major tasks in single-variable calculus are differentiation and integration and the fundamental theorem of calculus relates integration with antidifferentiation. Differentiation is the step for determining derivatives and its reverse process is known as antidifferentiation.
Moreover, in this article basic definitions, formulas, rules, and with the help of examples derivatives of different functions will be evaluated for your overall concept each example will be chosen from a different topic.
Differentiation
Differentiation is a function of a real variable f(x) is differentiable at point “x” of its domain if its domain contains an open interval I containing a, and the limit exists.
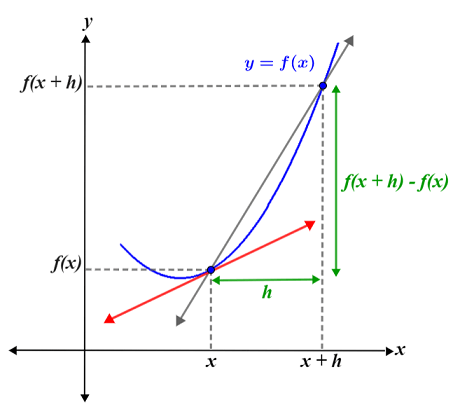
L = limh→0 [f(x + h) – f(x)]/h
Methods to find derivatives
1) Simple Differentiation
2) First Principal Rule
3) Partial differentiation
- Simple Differentiation
is a technique in which we find derivatives by using rules according to function demands algebraic expression power rule will be used and in multiply condition product rule will be used and if variables come in the division, then the quotient rule will be used.
Moreover, if it is difficult to find the derivative of a long statement question then you can take help from the substitution method and by using the chain rule easily you can calculate the derivative of complicated problems.
- First principal rule
It is a little bit lengthy method to find the derivative of the function and it can also use for taking the derivative of the function in this method, the binomial theorem will be used if the power or exponent of the function is positive, we apply the binomial theorem while if the power is negative or in fraction form then we use binomial series.
- Partial differentiation
It is also used for taking the derivative of the function it is used for more independent variables if a function is depending on more than one variable then problems can be differentiated partially moreover procedure for finding it is that it will take the derivative of the one variable and consider the other variable as a constant.
Example Section
In this section with the help of examples, derivatives will be evaluated by different techniques.
Example 1:
Evaluate the derivative of (x3+5x + 6) * (x+1)
Solution:
Step 1: Let the given function is y
y = (x3+5x + 6) * (x+1)
Step 2: Taking derivative on both sides with respect to x
d/dx (y) = d / dx {(x3+5x + 6) * (x+1)}
Step 3: As you see it is in product form the product rule will be used here to find the derivative
In simple words,
d/dx (y) = (1st Function as it is) * (Derivative of 2nd) + (2nd Function as it is) * (Derivative of 1st)
In mathematical form,
d/dx (y) = d/dx (A(x)*B(x)) = A(x) × d/dx (B(x)) + B(x) × d/dx (A(x))
dy /dx = (x3+5x + 6) × d/dx (x+1) + (x+1) × d/dx (x3+5x + 6)
Step 4: Here with help of the sum rule and power rule, you can easily calculate the derivative.
dy /dx = (x3+5x + 6) × {d/dx (x)+d/dx (1)} + (x+1) × {d/dx (x3) + 5 d/dx(x) + d/dx (6)}
dy /dx = (x3+5x + 6) × (1) + (x+1) × (3x2 + 5(1) + 0}
Step 5: Now simplify the terms to get your derivative of the given function.
dy /dx = (x3+5x + 6) + (x+1) × (3x2 + 5)
dy /dx = (x3+5x + 6) + 3x3 + 5x +3x2 + 5
dy /dx = x3+5x + 6 + 3x3 + 5x +3x2 + 5
dy /dx = 4x3+3x2+10x + 11
dy /dx = 4x3+3x2+10x + 11 is the required derivative of the function.
The above problem of differentiation can also be solved through online calculators to save time.
Problem solved through derivative calculator by Allmath (https://www.allmath.com/derivative.php)
Example 2:
Determine the derivative of function y = 3x2 + 1 by using the first principal rule.
Solution:
Let,
Y = 3x2 + 1
Step 1: Replace y with y + ẟy and x with x+ẟx
Y+ ẟy = 3 (x+ẟx)2 + 1
Step 2: Now simplifying the terms
ẟy = 3{(x)2+2x ẟx + (ẟx)2} + 1 – y where y = 3x2 + 1
ẟy = 3{(x)2+2x ẟx + (ẟx)2} + 1 – (3x2 + 1)
ẟy = 3{(x)2+2x ẟx + (ẟx)2} + 1 – 3x2 – 1
ẟy = 3{(x)2+2x ẟx + (ẟx)2} – 3x2
ẟy = 3x2+6x ẟx + 3(ẟx)2 – 3x2 cancelling 3x2
ẟy = 6x ẟx + 3(ẟx)2
Step 3: Taking common ẟx from right hand side
ẟy = ẟx {6x + 3(ẟx)}
Step 4: Divide by ẟx on both sides
ẟy / ẟx = ẟx {6x + 3(ẟx)} / ẟx
ẟy / ẟx = {6x + 3(ẟx)}
Step 5: Taking limit ẟx → 0
Lim ẟx → 0 ẟy / ẟx = Lim ẟx → 0 {6x + 3(ẟx)}
dy / dx = 6x + 3(0)
dy / dx = 6x
d / dx (3x2 + 1) = 6x
Example 3:
Find the partial derivative of function f (y, z) = 4y + 5z
Solution:
Step 1: Now to find the partial derivative of the variable y then consider the z variable as a constant
Thus, ∂f/∂y = 4
Step 2: Similarly, to find ∂f/∂z of the variable z then consider the y variable as a constant
Thus, ∂f/∂z = 5
Summary
In this article, the basic idea of derivative importance definition, formula, and different techniques used to calculate derivatives are discussed. Moreover, detailed concepts with the help of examples and also used different rules to find the derivatives are given.
We hope you can easily now solve the problems of derivatives with the help of these concepts about differentiation.